
Now, when we have defined our data, we can start off by creating the functions. When \(x \) is equal to 2 the \(y \) is equal to 4. Here we can see the relationship between \(x \) and \(y \).

scatter( x_data, y_data) Code language: CSS ( css ) As parameters we will pass the x_data and y_data variables. Now, we can scatter our data using the function plt.scatter(). The variable x_data represents the study time, and y_data represents the grades. Note that here we are using the same values as in the first example. Y_data = x_data * 2 Code language: PHP ( php ) Next, using the function np.array() we will create a variable named x_data which will be our intendent variable Also we will create a y_data variable, which will simply store the values of x_data multiplied by two. Import torch Code language: JavaScript ( javascript ) We will also import torch, which is the PyTorch module. We will start by applying an intuitive approach based on PyTorch, and then we will do a full implementation in PyTorch.įirst, let’s import the necessary libraries including NumPy and matplotlib. Now, let’s see how we can create a linear regression model in Python using PyTorch. In the following GIF animation the Gradient descent algorithm is visualized
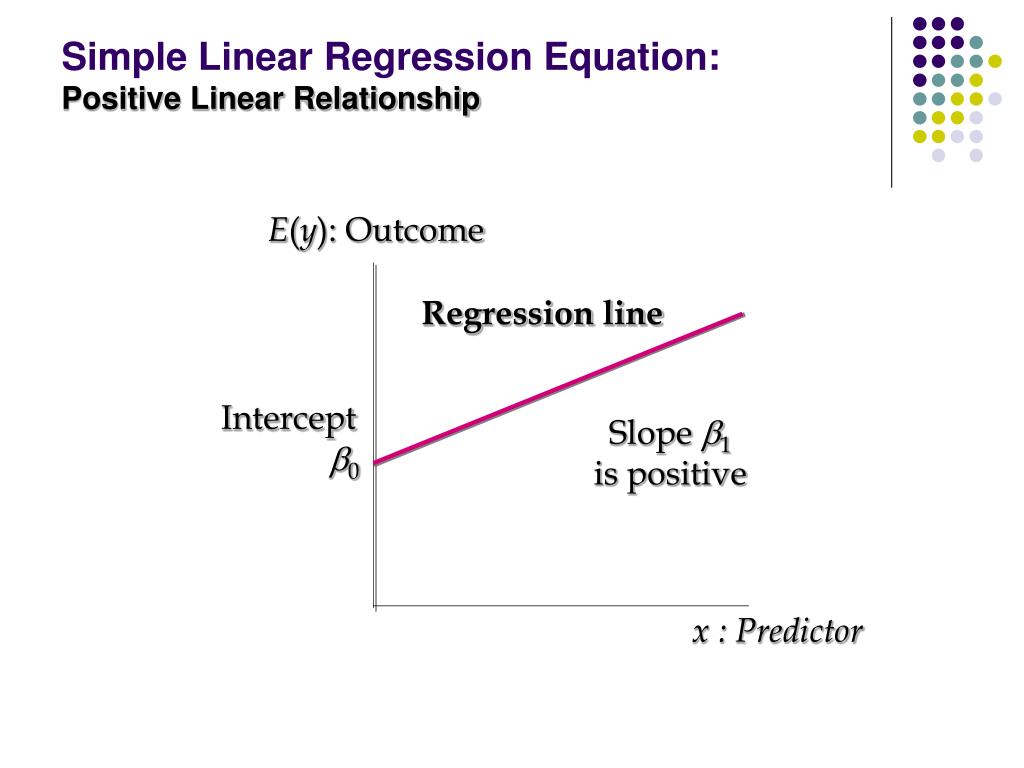
Hence, we computed the Global loss minimum. Once our gradient is close to zero the algorithm will stop and we will know the minimum value of \(w \). Then, we will continue to compute the gradient moving towards the minimum value of \(w \). So, based on this gradient, and \(\alpha \) we will move to the left. It is usually a very small value (\(\alpha=0.01 \)). The parameter \(\alpha \) (learning rate) will determine how much we need to move. Here we just subtracted our initial \(w \) with the gradient. We can say that \(w_ \) are the values of a single point measured data point. To better understand the process of determining optimal parameters \(w \) and \(b \), let’s first try to guess them. In that way we will be able to find a function of a line which will determine the optimal correlation between dependent and independent variables in our model. Therefore, the main goal of our analysis is to determine the values for \(w \) and \(b \). We can’t draw the line because the parameters \(w \) and \(b \) are unknown to us.


 0 kommentar(er)
0 kommentar(er)
